R E C - T E C
ACCIDENT . . . . . RECONSTRUCTION . . . . . . SOFTWARE

"when performance counts"

MEASURING LINEAR MOMENTUM ANGLES

Copyright Ó George M. Bonnett, J.D. 1997 All rights reserved.

Linear momentum angles have long been a thorn in the side of almost everyone attempting to investigate vehicular accidents. This single issue has probably accounted for more discussion than any other facet of linear momentum as related to accident reconstruction.

Approach angles are sometimes elusive, but there is little discussion about how the angle is obtained. The approach angle is the angle traveled by the center of mass of the respective vehicle at first contact. We may differ about the value of this angle, but all agree on what angle is being discussed and how to obtain it.

Why is this so? Is this the correct angle that should be used?

More on the approach angles later. It is the departure angles that present the real problems. How should they be measured?

One approach is measuring the angle from the center point of maximum engagement to the center of mass of the vehicle at the position of final rest. While incorrect, this is a commonly used approach by those unfamiliar with the laws of physics in general, and linear momentum in particular. This method has two errors as will be discussed later.

Another approach is to measure from the center of mass of the vehicle at maximum engagement to the center of mass at final rest. This method is also flawed as will be demonstrated.

How then should the angle be measured? Before answering that question let's define some terms.

• CENTER OF GRAVITY: That point at which the entire weight of an object may be considered concentrated; that is, the line of action of the body's weight passes through the center of gravity.

• CENTER OF MASS: The single point within a body that responds and is displaced in the same manner as a point mass would respond and be displaced when subjected to the same external forces. The force (f) is the product of the mass (m) and the acceleration (Acm) of the center of mass. Due to the uniform gravitational acceleration (g) acting on the body, the center of mass and the center of gravity coincide.

• CONSERVATION OF LINEAR MOMENTUM: If the resultant external force acting on a system of bodies is zero (0), the vector sum of the momenta of the objects will remain constant. In collision, the vector sum of the momenta just prior to impact equals the sum of the momenta just after impact.

• FINAL REST: That point at which the vehicle has come to a complete stop.

• LINEAR MOMENTUM: A vector quantity which is the product of a body's mass (m) and its velocity. The direction is that of the velocity.

• NEWTON'S FIRST LAW: An unaccelerated body remains unaccelerated unless it is caused to change that state by forces exerted on it by the environment.

• NEWTON'S SECOND LAW: The acceleration of a particle is equal to the ratio of the net force acting on the particle to the internal mass of the particle. A = f/m

• NEWTON'S THIRD LAW: To every action there is always opposed an equal reaction. The action forces and reaction forces are on different bodies.

• MAXIMUM ENGAGEMENT: The point at which a significant portion of both vehicles, at the collision interface, reach a common velocity.

Point mass physics is used in accident reconstruction to describe the motion of vehicles. The point used is the center of gravity (center of mass). If this point is used to measure the motion of the vehicle, it is apparent that the departure angle cannot be measured from the center point of maximum engagement. Measurement of the vector direction must be from the center of mass of the vehicle immediately after maximum engagement.

With this as our starting point, what is used as the second point in determining the line that will represent the vector direction? The vehicle comes to a stop at a given point. Why not use this point? Is it the point that should be used?

The fallacy of using final rest as the second point can be attacked using several different arguments:

1. Newton's first law - the vehicle is accelerated (deceleration) due to friction with the surface over which it travels from maximum engagement to final rest. In addition to a change in velocity, the vehicle may also be accelerated by a change of direction. The forces acting at the surface to surface interface between the vehicle and the surface over which it is traveling can, and often do, result in a change in both velocity and direction. The change in direction can result from a steering input, striking a curb, the crown of the roadway, differential braking that may result from damage, or any one of thousands of external forces. This change in direction has nothing to do with the forces acting on the vehicles in collision, and therefore nothing to do with the collision.
   
2. Conservation of Momentum - In the above definition, reference is made to the "momenta just after impact". It does not reference the acceleration (deceleration) after impact or the position at final rest.
   
3. Linear Momentum Formula - Inspection of the formula does not reveal a distance and direction. The formula refers to the momenta of the vehicle. Momenta is the mass (or weight) of the object multiplied by the velocity of the vehicle. The momentum vector is the mass times instantaneous velocity (length) and the angle (direction) associated with this velocity.

Post impact distance is used with the coefficient of friction between the objects to determine the post impact velocity. This is the velocity immediately after impact. The corresponding direction, or angle, is the direction just after impact (maximum engagement). This is the angle associated with the departure velocity.

The linear momentum formula does not call for the average velocity between maximum engagement and final rest, it uses an instantaneous post impact velocity. The angle required is the vector angle associated with this instantaneous post impact velocity vector. It would be just as inaccurate to use the average direction after impact as to use the average velocity. Using the final rest methodology would be analogous to using the direction from the starting point of any motion (parking place) to the point of first contact for the approach angle. It is easy to see the possibilities of inaccuracy using this method for the determination of the approach angles. The same is true for the departure angles.

In some cases the departure angles may be the same if measured just after impact or if measured to final rest. It is also possible that the approach angle measured from the start of the trip to first contact may be the same as the instantaneous angle at first contact, but this is not always true. They can be, and often are, different.

Approach angles have there own idiosyncrasies. What should be done about the slip angle or difference between the heading of the vehicle and the direction traveled by the center of mass? The answer is nothing. Linear momentum does not utilize slip angle. The approach angle is the instantaneous angle, at first contact, traveled by the center of mass of the respective vehicle. This is the vector direction of the center of mass at first contact.

CONCLUSION: The correct approach angle is the path taken by the center of mass of the vehicle in question at first contact. The correct departure angle is the path taken by the center of mass of the vehicle in question immediately after separating from the collision (maximum engagement), not to the final rest position. While it is often difficult to measure these angles, these are the ones required by the formula to meet the requirements for the use of Linear Momentum. Using any other angles can produce inaccurate results. These inaccuracies can be due to laziness, ignorance, stupidity (practiced ignorance), or even a deliberate attempt to deceive.

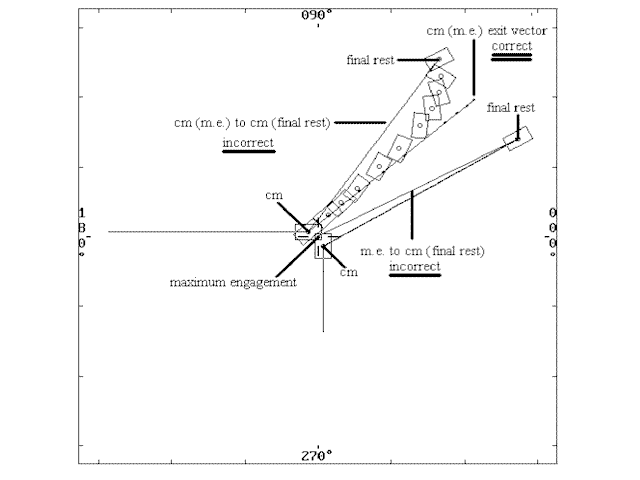
Figure 1:  This figure shows a collision diagram in which one of the vehicles spun out after impact.  If the departure angle were measured to final rest, it would vary significantly from the actual departure vector, which shows the correct angle for a zero restitution collision.  The correct departure angle for the other vehicle just happens to be the same as the line from the center of mass at separation to the center of mass at final rest since the vehicle traveled in a perfectly straight line.   If restitution is involved, maximum engagement will not coincide with the point of separation.  The departure angle at the instant of separation must be used for Linear Momentum.

1-321-639-7783

321-639-7783
Voice or Fax

Copyright Ó George M. Bonnett, J.D. 1997 All rights reserved.